Warm up for the brain: can you solve the counterfeit coin problem? Check it out!

The mathematician has only three attempts, so you can't weigh each coin separately. You need to divide them into piles and put them on the scales several pieces at a time, gradually getting closer to the fake one.

Let's say a mathematician decides to divide 12 coins into three piles of four coins each. Then he put four coins on each scale. This weighing can give two results. Let's consider each of them.

1. The weight of the two piles of coins was the same. Consequently, all the money in them is real, and the counterfeit lies somewhere among the four unweighted coins.

To track the result, the mathematician marks all scripts with a zero. Then he takes three of them and compares them with three unweighted coins. If their weight is equal, then the remaining (fourth) unweighted coin is counterfeit. If the weight is different, the mathematician places a plus on the three unmarked coins if they are heavier than those with zeroes, or a minus if they are lighter.

Then he takes two coinsmarked with plus or minus and compares their weight. If it is the same, then the remaining copy is a fake. If not, the mathematician looks at the signs: among the coins with a plus, the fake will be the one that is heavier, among the coins with a minus, the one that is lighter.

2. The weight of the two piles of coins was not the same.

In this case, the mathematician needs to act as follows: mark the money in a heavy pile with a plus, in a light pile - with a minus, in an unweighted pile - with a zero, since it is known that the fake copy was on the scales.

Now you need to regroup the coins to fit into the two remaining weighings. One of the ways is to take instead of three coins with a plus, three coins with a minus, and put three pieces with a zero in their place.

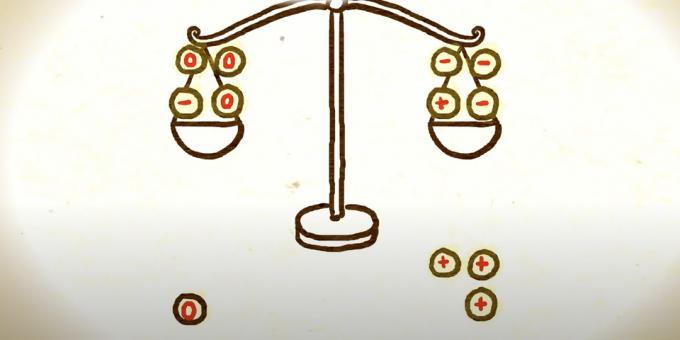
Three possible options follow. If that scale that was heavier still outweighs, then either the old coin with the plus sign on it is heavier than the rest, or the coin with the minus sign remaining on the other scale is lighter. A mathematician needs to choose any of them and compare with a common pattern to find a fake.

If the weighing pan, which was heavier, has become lighter, then one of the three coins with a minus sign moved by the mathematician is the lightest. Now he needs to compare two of them on the scales. If the results are tied, the third coin will be counterfeit. In case of inequality, the fake one is easier.

If the bowls are balanced after replacing, one of the three coins removed from the scales with a plus sign is heavier than the others. A mathematician needs to compare two of them. If they are equal, the third is fake. In case of inequality, the fake is the one that is heavier.

The emperor nods approvingly as he listens to the reasoning maths, but the dishonest governor goes to prison.

This puzzle is the translation of a TED-Ed video.