"Stoloto" says that the probability of winning has increased 5 times. We checked

And here is the probability calculation formula for the hypergeometric distribution:

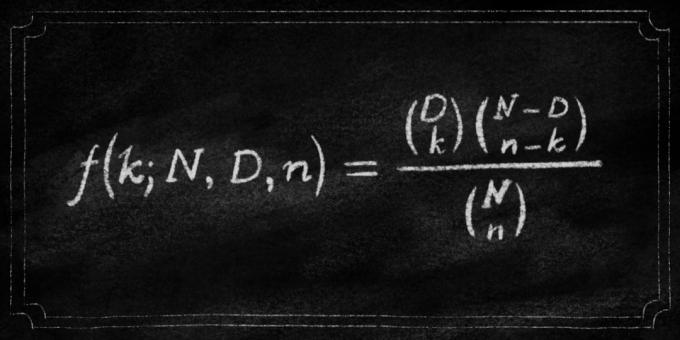
D - the number of winning numbers

N - number of lottery numbers in all

n - number of player selected numbers on the ticket,

k - the size of the winning combination.

How all this mean? What kind of braces?

Suppose that we have a lottery, where only 4 possible numbers, from which you can delete only 2 on the ticket. Select these numbers can be something like this:

Each column - a possible combination. Total turns 6 variants. It is called the number of combinations from 4 to 2. Cunning people figured out how to calculate it for any amount of numbers in the lottery and the number of numbers that can be deleted in the ticket. Decided that the record will be as follows:

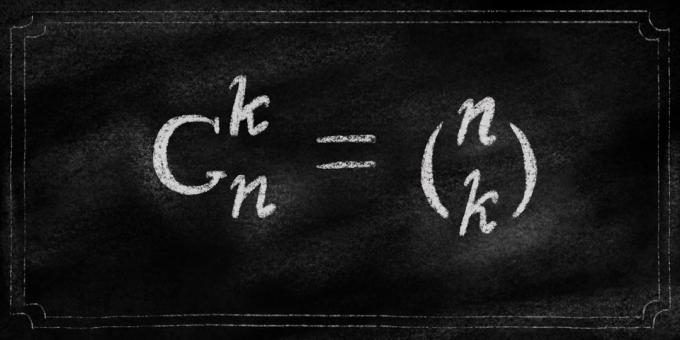
We will write this as C (n, k). In our case - C (4,2) = 6. Just the very parenthesis of the probability formula for the hypergeometric distribution. Now is the time to look at it with new eyes. It is written here in this form:

f (k, N, D, n) = C (D, k) * C (N-D, n-k) / C (N, n)

It could be considered:

C (N, n) - for example, the player has a ticket with the numbers (1,2,3,4,5,6,7). This is only one of 49 possible combinations of numbers in the lottery. And such combinations all theoretical can be C (N, n) = C (49,7). That is, this number shows how many different winning combinations can all be in the lottery.

C (D, k) - e.g., a winning combination of numbers 7 - (1,4,7,12,55,44,33). And we look at all the possible combinations of pairs - (1.4) (1.55) (12.33)... These combinations theoretically possible total C (D, k) = C (7,2). For now, just remember.

C (N-D, n-k) - The most interesting. For example, we have a winning pair (1,4). Then all the other numbers can be anything, not just winning. E.g., (1,4,3,2,5,6,8). We need to calculate how many ways we can choose the remaining 5 of the 42 numbers that are guaranteed to lose. In this case C (N-D, n-k) = C (49-7,7-2).

So we thought all combinations for only one of the winning combinations. But it should be something for everyone. Therefore, to get the total number of winning combinations, we multiply each other C (D, k) and C (N-D, n-k).

A more simple. Divide the winning combination for all theoretically possible to get a chance of winning a winning combination of size k. In this example, k = 2, but it may be 3, 4, 5... You're just count all lottery winning combinations:

For k = 2: f (2,49,7,7) = C(7,2)* C(49-7,7-2)/ C(49,7) = 0,2080

For k = 3: f (3,49,7,7) = C(7,3)* C(49-7,7-3)/ C(49,7) = 0,0456

For k = 4: f (4,49,7,7) = C(7,4)* C(49-7,7-4)/ C(49,7) = 0,0047

Then you can not count, because the probability is too low. So put all these probabilities, and we obtain f ([2,3,4], 49,7,7) = 0,2583. And now the moment of truth. Take the declared exponent 1 / 3.9, produce division and get 0.2564 - a number close probability 0.2583. Well, the statement "Stoloto" seems to be true!