5 logic puzzles to find patterns

Instead of a question mark, the circle should contain the number 253. This is the principle by which numbers in circles are formed: each previous one is multiplied by 2, and 3 is added to the result.

1 × 2 + 3 = 5.
5 × 2 + 3 = 13.
13 × 2 + 3 = 29.
29 × 2 + 3 = 61.
61 × 2 + 3 = 125.
125 × 2 + 3 = 253.

Or here's another way of solving: to each previous number, 2 is added to the n-th power.

1 + 2² = 1 + 4 = 5.
5 + 2³ = 5 + 8 = 13.
13 + 2⁴ = 13 + 16 = 29.
29 + 2⁵ = 29 + 32 = 61.
61 + 2⁶ = 61 + 64 = 125.
125 + 2⁷ = 125 + 128 = 253.

Instead of a question mark, the letter "P" should be in the square. The sum of the numbers in each square is the ordinal number of the letter in the alphabet. Let's check:

6 + 4 + 4 = 14. "M" is the fourteenth letter in the alphabet. We also count "Yo"!
4 + 1 + 7 = 12. "K" is the twelfth letter in the alphabet.
5 + 6 + 10 = 21. "U" is the twenty-first letter in the alphabet.
1 + 14 + 2 = 17. "P" is the seventeenth letter in the alphabet, which should be in place of the question mark.

Instead of a question mark, the number 179 should be. If you move clockwise starting from 3, then each subsequent number is equal to twice the previous one, to which 1, 3, 5, 7, 9 were added.

3 × 2 + 1 = 7.
7 × 2 + 3 = 17.
17 × 2 + 5 = 39.
39 × 2 + 7 = 85.
85 × 2 + 9 = 179.

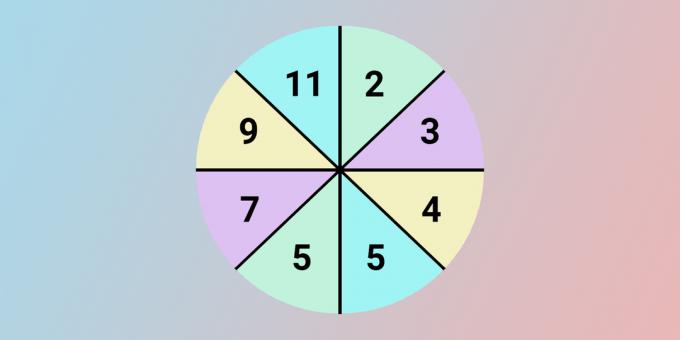
Instead of a question mark, there should be the number 11. To get each number from the left half of the circle, we take the number from the opposite sector, double and add one.

5 = 2 × 2 + 1.
7 = 3 × 2 + 1.
9 = 4 × 2 + 1.
11 = 5 × 2 + 1.

Instead of a question mark, the number should be 66. If you move clockwise starting from 4, each subsequent number is equal to twice the previous one, from which two was subtracted.

4 × 2 − 2 = 8 − 2 = 6.
6 × 2 − 2 = 12 − 2 = 10.
10 × 2 − 2 = 20 − 2 = 18.
18 × 2 − 2 = 36 − 2 = 34.
34 × 2 − 2 = 68 − 2 = 66.