7 ways to find the area of ​​a rectangle

1. If two adjacent sides are known

Just multiply the two sides of the rectangle.

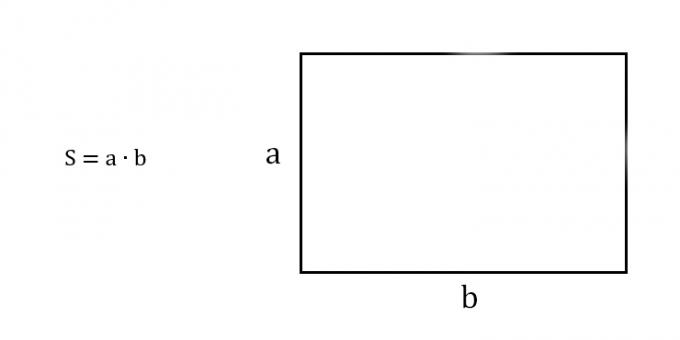
• S is the required area of ​​the rectangle;
• a and b are adjacent sides.

2. If any side and diagonal are known

Find the squares of the diagonal and either side of the rectangle.

Subtract the second from the first number and find the root of the result.

Multiply the length of the known side by this number.

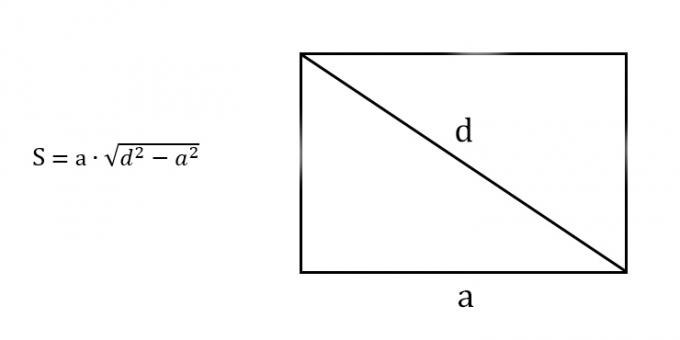
• S is the required area of ​​the rectangle;
• a - known side;
• d - any diagonal (recall: both diagonals of a rectangle have the same length).

3. If any side and diameter of the circumscribed circle are known

Find the squares of the diameter and either side of the rectangle.

Subtract the second from the first number and find the root of the result.

Multiply the known side by the resulting number.

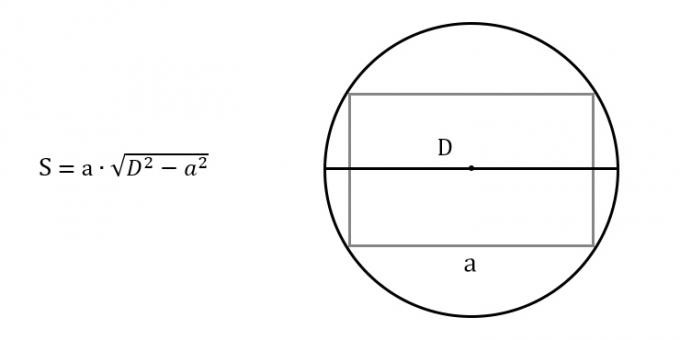
• S is the required area of ​​the rectangle;
• a - known side;
• D is the diameter of the circumscribed circle.

4. If any side and radius of the circumscribed circle are known

Find the square of the radius and multiply the result by 4.

Subtract the square of the known side from the resulting number.

Find the root of the result and multiply the length of the known side by it.

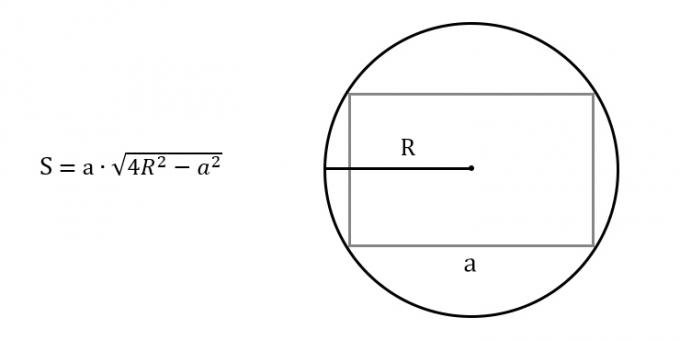
• S is the required area of ​​the rectangle;
• a - known side;
• R is the radius of the circumscribed circle.

5. If any side and perimeter are known

Multiply the perimeter by the length of the known side.

Find the square of the known side and multiply that number by 2.

Subtract the second from the first product and divide the result by 2.

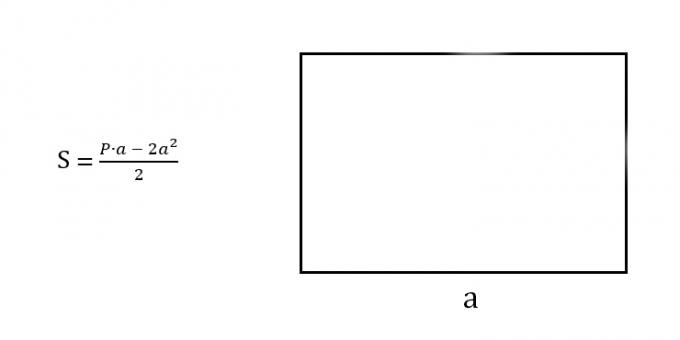
• S is the required area of ​​the rectangle;
• a - known side;
• P - perimeter of the rectangle (equal to the sum of all sides).

6. If the diagonal and the angle between the diagonals are known

Find the square of the diagonal.

Divide the resulting number by 2.

Multiply the result by the sine of the angle between the diagonals.

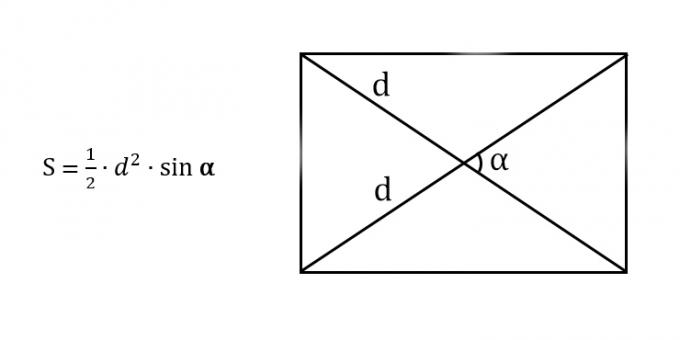
• S is the required area of ​​the rectangle;
• d - any diagonal of the rectangle;
• α is any angle between the diagonals of the rectangle.

7. If the radius of the circumscribed circle and the angle between the diagonals are known

Find a square circle radiuscircumscribed around a rectangle.

Multiply the resulting number by 2, and then by the sine of the angle between the diagonals.

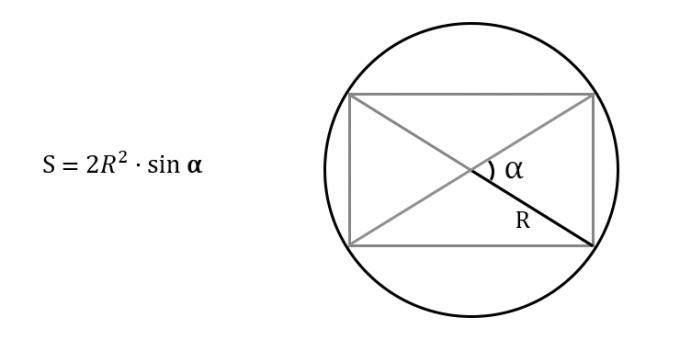
• S is the required area of ​​the rectangle;
• R is the radius of the circumscribed circle;
• α is any angle between the diagonals of the rectangle.