9 logical tasks that the teeth only intellectuals
Forming Educational Program / / December 19, 2019
1. Birthday Cheryl
Suppose some Bernard and Albert recently met with the girl Cheryl. They want to know when her birthday - to prepare the gifts. But Cheryl is the more little thing. Instead of answering, she gives the guys a list of 10 possible dates:
| May 15 | 16th of May | May 19 |
| June 17 | June 18th | |
| the 14 th of July | July 16 | |
| August 14th | August 15 | August 17th |
Predictably discovered that the young man can not calculate the correct date, Cheryl whisper in his ear, Albert calls only a month of her birth. And Bernard - also quiet - just a number.
- Hmm, - says Albert. - I do not know when Cheryl's birthday. But I do know that Bernard does not know this.
- Ha - meets Bernard. - At first I did not know when Cheryl's birthday, but now I know it!
- Yeah, - agrees Albert. - Now, I know that, too.
And they called in unison certain date. When Cheryl birthday?
If you are not able to go to find the answer, do not worry. For the first time this question was asked in the teenage Mathematical Olympiad in SingaporeSingapore and Asian School Math Olympiad
Which is famous for the highest educational standards. Once one of the local presenters published this screen puzzles to Facebook, it became viralWhen is Cheryl's birthday? 'The tricky maths problem that has everyone stumped: Solve it tried to tens of thousands of users of Facebook, Twitter, Reddit. But all have failed.We are confident that you'll get. Otgadku not open until at least do not try.
View the answer.
Hide.
July 16. This follows from the dialogue that took place between Albert and Bernard. Plus a little process of elimination. See.
If Cheryl was born in May or June, so her birthday can be 19th or 18th. These numbers are found in only one time list. Accordingly, Bernard, hearing them, just could see about a month in question. But Albert, as follows from its first replica, I'm sure Bernard, knowing the number, definitely will not be able to call a month. So, we are not talking about May or June. Cheryl was born in the month, each of these dates in which there is a double in the adjacent months. That is - in July or August.
Bernard, who knows of birth, hearing and analyzing replica Albert (that is, finding out about July or August), says that now knows the correct answer. From this it follows that a certain number of Bernardo - not 14, because it is duplicated, and in July and August, so it is impossible to determine the correct date. But Bernard confident in his decision. So, the number known to him does not double in July and August. Under this condition get three options: 16 July, 15 August and 17 August.
In turn, Albert heard the words of Bernard (and logically before reaching the above-mentioned three possible dates), stated that now also knows the correct date. We remember that Albert is known for a month. If this month was August, the young man could not determine the number of - in fact, in August featured just two. So, there is only one option - 16 July.
2. How old daughters
On the street one day, two former classmates met and held a dialogue between them.
- Hi!
- Hi!
- How are you?
- Good. Grow two daughters, doshkolnitsy more.
- And how old are they?
- Well-at... the product of their ages is equal to the number of pigeons at our feet.
- This information is not enough for me!
- senior like her mother.
- Now I know the answer to your question!
So how many years daughters one of the interlocutors?
View the answer.
Hide.
1 and 4 years. Since the answer became clear only after receiving information that one of the daughters of older, so before there was ambiguity. At first, based on the number of pigeons, the variant that the daughters - twins (that is, their ages are equal). This is only possible with the number of pigeons is the square numbers up to and including 7 (7 years old - the age when children go to school, that is, cease to be preschoolers): 1, 4, 9, 16, 25, 36, 49.
From these squares, only one can be obtained by multiplication of two different numbers, each of which is equal to or less than 7, 4 - (1 × 4). Accordingly, the daughters of 1 and 4 years. Other whole while "pre" There is no alternative.
3. Where is my car?!
They say the problem is given by the students of junior classes of Hong Kong schools. Children decide it is literally in seconds.
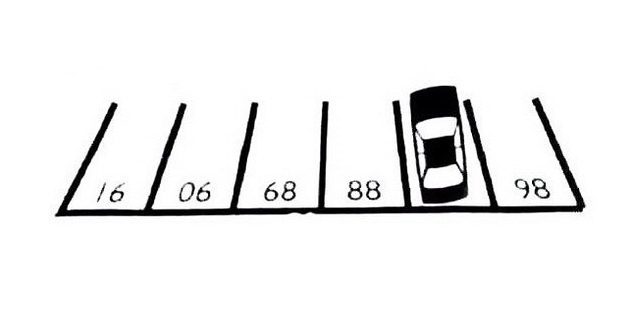
Name the number of parking spaces, which takes the car.
View the answer.
Hide.
87. To guess, just look at the picture on the other side. Then the numbers that you see now upside down, take the right position - 86, 87, 88, 89, 90, 91.
4. Love in Kleptopii
Jan and Maria love each other, communicating only through the Internet. Jan wants to send Mary a wedding ring in the mail - to make an offer. But here's the rub: beloved country live in Kleptopii where any parcel transmitted by mail, is bound to be stolen - if it is not enclosed in a box with a lock.
At John and Mary's many castles, but send each other keys, they can not - because the keys will also be stolen. How to send Jan ring to it certainly has got into the hands of Mary?
View the answer.
Hide.
Yang should send Maria a ring in a locked box. Without the key, of course. Maria received the parcel, should be embedded in her own castle.
Then Jan sent a box again. He opened his own key and lock re-addresses the parcel with the only remaining locked lock Mary. And the girl is the key to it.
Incidentally, this task - not just a theoretical game of logic. Used in its idea - a fundamentalSeven Puzzles You Think You Must Not Have Heard Correctly Key Exchange cryptographic principle of Protocol Diffie - Hellman. This protocol enables two or more parties to get the shared secret key over an insecure communications channel listening.
5. In search of forgery
The courier brought you 10 bags, each with a lot of coins. And all would be good, but you suspect that the money in one of the fake bags. All you know for sure - that's what real coins weigh 1 g each, and fake - 1.1 g Other differences between the money there.
Fortunately, you have an accurate digital scale, showing the weight of up to a tenth of a gram. But the courier in a hurry.
In short, no, you are given only one attempt to use weights. As in one weighing accurately calculate in which one bag are fake coins and whether there is such a bag at all?
View the answer.
Hide.
One weighing enough. Just put on the scales just 55 coins: 1 - from the first bag, 2 - in the second, 3 - in the third, four - from the fourth... 10 - from the tenth. If the whole bunch of money will weigh 55 g - so fake is not in one of the bags. But if the weight will be different, you will immediately understand what the serial number of bags full of fakes.
Consider if indications of weights will differ from the reference 0.1 - counterfeit coins in the first bag, 0.2 - in the second, 0.3 - in the third... 1.0 - a tenth.
6. equality tails
In the dark-dark (now do not see any DIG, and you can not turn on the light), the room is a table on which are 50 coins. You do not see them, but you can touch, flip. And most importantly, know exactly: 40 coins originally lies eagle up, and 10 - tails.
Your task - to share money into two groups (not necessarily equal) each of which is the same number of coins up tails.
View the answer.
Hide.
Divide the coins into two groups: one 40, the other 10. Now turn all the money from the second group. Voila can include light: the task is completed. Do not believe me - check.
For pedants mathematicians explain the algorithm. After the blind separation into two groups here is what happened: the first left's tails; and second, respectively, - (10 - x) tails (for a total of 10 conditions tails problem). A eagles thus - 10 - (10 - x) = x. That is, the number of eagles in the second group is the number of tails in the first.
Do simple step - turn over all the coins in the second bunch. Thus, all coin-eagles (pieces) are coins-tails, and their number is the same as the number of tails in the first group.
7. How not to get married
Once the owner of small shops in Italy owes a large sum to the moneylender. The possibility to repay a debt he did not. But there was a beautiful daughter, who has long loved the lender.
- Let's do so, - has offered the shopkeeper the moneylender. - You vydaosh daughter to me, and I remember as a relation of duty. Well, on the hands?
But the girl did not want to get married an old and ugly man. Therefore, the shopkeeper refused. However, a potential son-catch in his voice swings and made a new proposal.
- I do not want to force anyone - said the usurer softly. - Let all of us to solve the case. Look, I'll put in the bag two stones - black and white. And let my daughter without looking pulls out one of them. If it is black, we had married, and I forgive you the debt. If White - I forgive the debt just like that, without having to hand your daughter.
The deal seemed fair, and this time my father agreed. Moneylender bent over to the track strewn with gravel, quickly picked up the stones and put them in a bag. But the daughter saw a horrible thing: the two were black pebble! Whatever it is pulled out, she would have to marry. Of course, it was possible to expose the moneylender in deception, taking both at the same stone. But that could come into a rage and cancel the transaction by requesting a debt in full.
After thinking for a few seconds, she confidently held out her hand to the pouch. And I did something that saved her father from debt, and it itself - the need for marriage. Justice moneylender even acknowledged her act. What exactly did she do?
View the answer.
Hide.
She pulled out a stone, and without having to show anyone, if accidentally dropped it on the track. Stone then mixed with the rest of the pebbles.
- Oh, I'm so clumsy! - clasped hands shopkeeper's daughter. - But that's nothing. After all, we can look in the bag. If there was a white stone, so I pulled the black. And vice versa.
Of course, when all looked in the bag, there was discovered a black stone. Even moneylender I had to agree: it means that the girl pulled the white. And if so - the wedding will not be and have to forgive the debt.
8. You have confused the code ...
You closed the suitcase on a digital lock with three-digit code numbers and accidentally forgotten. But memory It offers the following tips:
- 682 - this code is one of the numbers is correct and is in its place;
- 614 - one of the numbers correct, but should not in place;
- 206 - correct two digits, but the two are not in place;
- 738 - all nonsense, no one hit;
- 870 - One figure is correct, but not in its place.
This information is enough to find the right code. What is it?
View the answer.
Hide.
042.
Following the fourth tip, cross out all of the combinations of the numbers 7, 3 and 8 - they are in the desired code is definitely not. We find out from the first hint that his place is either 6 or 2. But if it is 6, it is not the condition of the second clue where 6 stands at the beginning. So, the last digit of the code - 2. A 6 is absent in the cipher.
From the third clue we conclude that the right numbers of the code - 2 and 0. In this case 2 is at the bottom. This means that the 0 - on the ground. Thus, we become aware of the first and third digits of the code: 0... 2.
Is compared to the second clue. Figure 6 shallows before. The unit does not fit: it is known that it is not on its place, but all the possible locations for it - first and last - are already occupied. Thus, the true figure is only 4. It and move into the middle of the resulting code - 042.
9. How to divide the cake
And finally, a little sweet. You have torteWhich should be divided by the number of guests - 8 pieces. The only problem is that it needs to be done, having made just three cuts. To the right?
View the answer.
Hide.
Make two cuts crosswise - as if you want to divide the cake into four equal parts. A third incision swipe not vertically but horizontally along the dividing treat.

see also🔎🤓✌️
- 10 tasks on logic and intelligence
- 4 explain the main logic of the law on the simple examples
- 5 effective tools for the development of creativity
- Solve 3 puzzles trick and find out how smart you are
- 10 tricky tasks to test logic and wit



